Validation par l’erreur totale¶

La validation¶
Différents textes réglementaires encadrent les bonnes pratiques de validation des méthodes analytiques GLP, GMP, GCP, et autres) ainsi que des textes normatifs (ISO, ICH, EMEA, et FDA) qui suggèrent tous que les procédures analytiques doivent se conformer à un critère d’acceptation. Cette demande impose donc que ces procédés soit validés. Plusieurs documents définissent les critères de validation à tester, mais aucun d’entre eux ne propose d’approche expérimentale et se limitent la plupart du temps à des concepts généraux. C’est pourquoi les membres de la SFSTP ont contribué à l’élaboration d’une méthode de validation pour aider l’industrie pharmaceutique à valider leurs procédures analytiques.
Cette approche permet de réduire considérablement le risque d’accepter une procédure qui ne serait pas suffisamment précise, ou à l’inverse, de rejeter une procédure qui serait satisfaisante.
La méthode du profil d’exactitude, utilise le vocabulaire normatif de l’ISO et propose une stratégie expérimentale de validation des procédures analytiques, indépendante du secteur industriel, pour utiliser de manière optimale les expériences réalisées de manière à extraire un maximum d’informations des résultats et pour minimiser le risque de réanalyser les échantillons en routine.
Objectifs d’une procédure analytique¶

Afin de décrire les objectifs d’une méthode analytique, il est nécessaire de revenir sur sa nature. Son objectif est-il de démontrer une variation de la réponse linéaire en fonction de la concentration ? Que le biais et la fidélité sont inférieurs à x%, ou encore de quantifier précisément une quantité inconnue ? Ces interrogations semblent pertinentes. L’objectif d’une procédure analytique est d’être capable de quantifier aussi précisément que possible une quantité inconnue que le laboratoire doit déterminer. En d’autre termes, ce que l’analyste recherche, c’est que l’écart entre la valeur mesurée \(x\) et la valeur vraie \(\mu_T\) (qui ne sera jamais connue), est aussi faible que possible, ou au moins inférieure à une limite acceptable. Cette exigence peut être exprimée par la relation suivante :
où \(\lambda\) est la limite d’acceptation qui dépendra des besoins de l’analyste ou des objectifs de la procédure analytique. En fait, la limite d’acceptation peut varier en fonction de l’usage envisagé de la méthode analytique (par exemple 1% à 2% pour des composés pharmaceutiques, 5% pour la détermination de substances actives ou 15% pour les bioanalyses).
Les principaux concepts ont été introduits, pas uniquement la limite d’acceptation pour la performance, mais aussi la responsabilité de l’analyste, de prendre la décision d’accepter la performance d’une méthode en fonction de son utilisation.
Les méthodes analytiques se caractérisent par deux types d’erreurs :
erreur systématique ou biais \(\mu_M\)
une erreur aléatoire évaluée par un écart-type \(\sigma_M\)
Une estimation du biais et de la variance de la méthode peut être obtenue par l’expérimentation lors de la validation. La fiabilité de ces estimations dépend de l’adéquation des mesures effectuées sur des étalons de validation, la conception expérimentale et le nombre de répétitions de mesures au cours de la phase de validation. Sur la base de ces estimations du biais et de la variance, il est possible de définir si la méthode est bonne en comparant la performance de la méthode à une limite d’acceptation \(\lambda\), définie pour un champ d’application donné (par exemple une analyse biopharmaceutique).
L’exemple ci-dessous représente la mise en application du critère d’acceptation pour différentes configurations de biais et de fidélité.
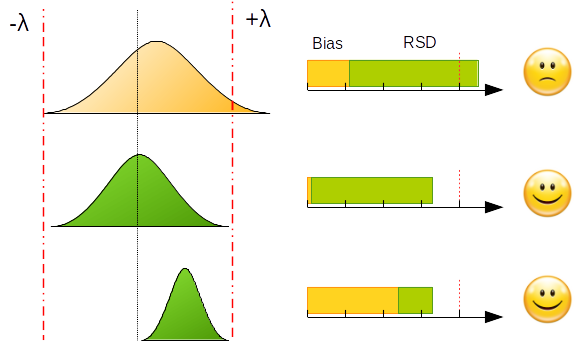
Souhaiter développer une procédure sans biais et sans erreur a un coût non négligeable. Cet objectif est irréaliste pour un analyste qui a généralement trop peu de temps pour optimiser tous les paramètres analytiques dans la phase de développement, même si l’utilisation de plans d’expériences est recommandée et bien décrite dans la littérature.
Pour surmonter ce dilemme, l’analyste devra prendre des risques minimes (ou tout au moins compatibles avec les objectifs d’analyse). Pour maîtriser ce risque, le raisonnement peut être inversé. On peut fixer comme hypothèse de départ que la méthode est acceptée si on peut garantir une proportion maximale (au pire des cas) de mesures en dehors des limites d’acceptation. Par exemple, au maximum 5% ou 20% des mesures à l’extérieur des limites d’acceptation. Cette proportion constitue, par conséquent, le risque maximal que l’analyste est prêt à prendre. La proportion désirée dépendra évidemment des objectifs de la procédure analytique.
Une procédure peut être valide s’il est très probable, que la différence entre chaque mesure \(x\) d’un échantillon et de sa vraie valeur \(\mu_T\) est à l’intérieur des limites d’acceptation prédéfinies par l’analyste. Ce concept peut être décrit par l’expression suivante:
avec \(\beta\) la proportion de mesures à l’intérieur de limites d’acceptation et \(\lambda\) les limites d’acceptation fixées a priori par l’analyste en fonction des objectifs de la méthode. La proportion de valeurs attendues à l’extérieur des limites d’acceptation évalue le risque de la procédure analytique.
Objectifs de la validation¶
L’objectif de la validation est de donner aux laboratoires ainsi qu’aux organismes de réglementation, la garantie que chaque mesure qui sera effectuée à l’avenir lors d’analyse en routine, sera assez proche de la vraie valeur (inconnue) de l’échantillon à analyser, ou au moins que la différence sera inférieure à celle d’une limite acceptable compte tenu de l’utilisation prévue de la méthode.
Les objectifs de la validation sont donc de réduire au minimum le risque pour le consommateur, ainsi que le risque du producteur. Par conséquent, l’objectif de la validation ne peut pas être simplement limité à l’obtention d’estimations de biais et la variance, mais doit se concentrer sur l’évaluation des risques même si ces estimateurs sont nécessaires pour évaluer le risque. En ce qui concerne cet objectif, deux notions de base mentionnées ci-dessus doivent être expliquées: assez proche, signifie par exemple, que la mesure réalisée en routine sera à moins de \(x \%\) de la valeur vraie (inconnue), ce qui signifie que la mesure, sera assez proche de la vraie valeur .
A cet égard, la justesse, la fidélité, la linéarité, … ne sont plus des statistiques permettant de quantifier ces garanties. En fait, on attend d’une méthode d’analyse d’être en mesure de quantifier et non pas d’être précise, même si la fidélité accroît incontestablement la probabilité d’être valide. Dans cette perspective, il est nécessaire de différencier les statistiques qui permettent de prendre une décision (par exemple, la procédure peut être considérée comme valide ou non sur la base de son aptitude à quantifier) et celles qui permettent de faire un diagnostic (par exemple, les tests statistiques évaluent la pertinence du modèle de régression ou l’homogénéité des variances).
En fait, les outils de décision adaptés sont vraiment nécessaires pour donner la garantie que les futures mesures seront raisonnablement à l’intérieur des limites d’acceptation. Si les garanties offertes par la règle de décision ne sont pas satisfaisantes, les outils de diagnostic aideront l’analyste à identifier les causes possibles du problème; mais seulement si les garanties ne sont pas satisfaites.
Règles de décision¶
L’examen de la situation actuelle, en ce qui concerne les règles de décision utilisées dans la phase de validation, montre que la plupart d’entre elles sont basées sur l’utilisation de l’hypothèse nulle de la manière suivante.
avec le \(\text{biais} = x-\mu_T\), le \(\text{biais relatif} = \frac{x - \mu_T }{\mu_T} \cdot 100\) et le \(\text{recouvrement} = \frac{ x}{\mu_T} \cdot 100\)
Sur cette base, une procédure est déclarée valide, si l’intervalle de confiance à 95%, du biais moyen comprend la valeur de 0 (0%. et 100%. dans le cas du biais relatif et le recouvrement, respectivement). Cependant, ce test est insuffisant dans le cadre de la validation des méthodes d’analyse, car la décision se fonde uniquement sur le calcul des critères de rejet du test t de Student. On ne prend pas en compte la finalité de la méthode analytique pour déterminer le critère d’acceptation. De plus, on remarque que deux conditions contribuent à valider à tort une méthode : les cas où l’écart-type est important (forte variabilité) et un nombre faible de répétitions de mesures.
Le fait de travailler avec les limites \(\pm \lambda\) permet d’éviter de rejeter une méthode dans le cas d’un écart-type faible et un biais faible, mais aussi d’accepter une méthode dont l’écart-type est élevé avec un biais important. Ceci nous montre également que l’utilisation du test d’hypothèse nulle est insuffisante dans le cadre de la validation des procédures analytiques. Le critère d’acceptation est un compromis entre biais et variabilité de telle sorte qu’une proportion donnée des mesures, choisie a priori, se trouve dans l’intervalle \(\pm \lambda\).
Cette dernière règle de décision apparaît nettement plus pertinente que la précédente puisque toutes les procédures ayant une faible dispersion de mesure sont acceptées, alors que les procédures ayant une forte dispersion sont rejetées. En outre, si une procédure a un biais, il devra avoir une faible dispersion pour être accepté. Symétriquement, une procédure avec une dispersion élevée devra avoir un faible biais pour être acceptée.
Malheureusement ces tests d’hypothèse restent largement utilisés, comme par exemple pour tester l’égalité des pentes d’étalonnage, la nullité de l’ordonnée à l’origine ou encore l’ajustement d’une droite de régression etc. Avec tous ces tests statistiques, moins la procédure est fidèle, plus la chance de succès est importante. Cette situation n’est certainement pas celle attendue par l’analyste qui exploite les statistiques pour évaluer la performance de la méthode analytique.
Dans ce contexte, une règle de décision simple et visuelle, consiste en l’utilisation d’un profil d’exactitude avec des limites d’acceptation relatives \(\pm \lambda\).
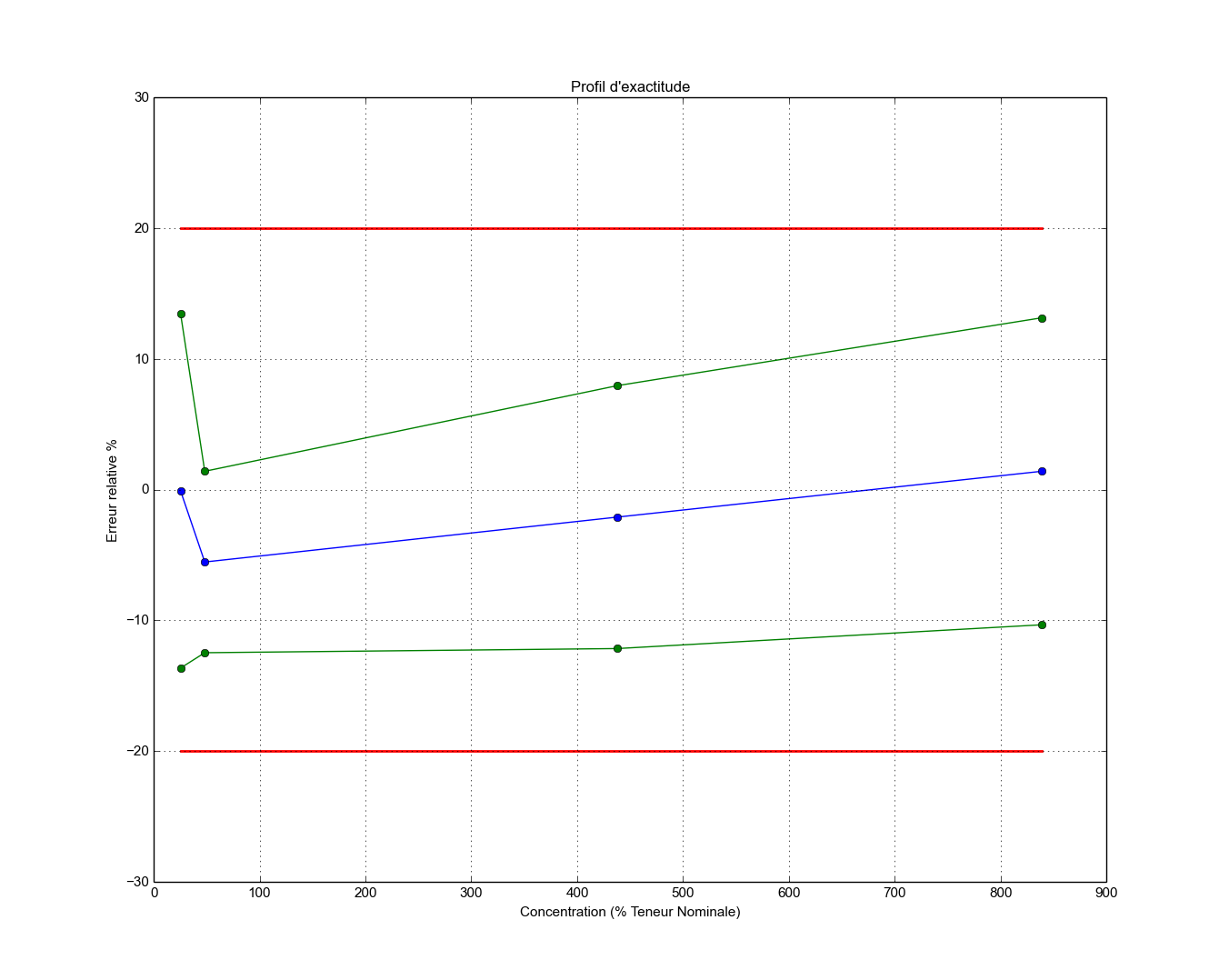
Profil d’exactitude réalisé avec SOSstat VPAQ¶
Le profil d’exactitude, construit à partir des intervalles de confiance sur les mesures attendues (ou intervalle statistique de dispersion), permet de décider de la capacité ou non d’une procédure d’analyse pour donner des résultats à l’intérieur des limites d’acceptation. Le profil d’exactitude décrit la plage dans laquelle la procédure est en mesure de quantifier avec une précision connue et un risque fixé a priori par l’analyste. Pour un risque assumé de 5%, par exemple, l’analyste peut garantir que 95 fois sur 100 les futures mesures données par sa procédure seront incluses dans les limites d’acceptation fixées en fonction des exigences réglementaires (par exemple: 1% ou 2% en volume, de 5% sur les spécialités pharmaceutiques, 15% en bioanalyse, environnement, etc.). Le profil est construit à partir des estimations du biais et de la fidélité de la procédure analytique, ainsi que l’intervalle de confiance, pour chaque niveau de concentration à la fin de la phase de validation. Cet intervalle de confiance est aussi appelé \(\beta\) -expectation tolerance interval. Il définit l’intervalle dans lequel tombera la proportion attendue des futurs résultats. Cet intervalle de tolérance obéit à la propriété suivante:
où E est l’espérance d’un résultat.
Le calcul de l’intervalle de confiance ou \(\beta\) -expectation tolerance interval exige l’estimation du biais et de l’écart-type de fidélité intermédiaire respectivement noté \(\mu_M\) et \(\sigma_M\).
Le profil d’exactitude peut être obtenu simplement en reliant les limites inférieures ou supérieures de l’intervalle de tolérance. Si une tolérance dépasse une limite d’acceptation, de nouvelles limites de quantification sont alors définies : LOQ (Limit of Quatification), ULQ (Upper limit of quantification ) et LLQ (Lower Limite of Quantification). Celles-ci se trouvent en parfait accord avec la définition de ce critère, à savoir, la plus petite quantité de la substance à analyser qui peut être mesurée avec exactitude et une fidélité définie.
Comme on le voit, le profil d’exactitude est un outil de prise de décision simple d’utilisation, qui permet non seulement de concilier les objectifs de la procédure avec ceux de la validation, mais aussi d’appréhender visuellement l’aptitude de la procédure analytique à tenir ses objectifs.
Définitions de l’ICH¶
Analytical procedure¶
The analytical procedure refers to the way of performing the analysis. It should describe in detail the steps necessary to perform each analytical test. This may include but is not limited to: the sample, the reference standard and the reagents preparations, use of the apparatus, generation of the calibration curve, use of the formulae for the calculation, etc.
Specificity¶
Specificity is the ability to assess unequivocally the analyte in the presence of components which may be expected to be present. Typically these might include impurities, degradants, matrix, etc. Lack of specificity of an individual analytical procedure may be compensated by other supporting analytical procedure(s).
Accuracy¶
The accuracy of an analytical procedure expresses the closeness of agreement between the value which is accepted either as a conventional true value or an accepted reference value and the value found. This is sometimes termed trueness.
Precision¶
The precision of an analytical procedure expresses the closeness of agreement (degree of scatter) between a series of measurements obtained from multiple sampling of the same homogeneous sample under the prescribed conditions. Precision may be considered at three levels: repeatability, intermediate precision and reproducibility.
Repeatability : Repeatability expresses the precision under the same operating conditions over a short interval of time. Repeatability is also termed intra-assay precision .
Intermediate precision :Intermediate precision expresses within-laboratories variations: different days, different analysts, different equipment, etc.
Reproducibility Reproducibility expresses the precision between laboratories (collaborative studies, usually applied to standardization of methodology).
Detection limit¶
The detection limit of an individual analytical procedure is the lowest amount of analyte in a sample which can be detected but not necessarily quantitated as an exact value.
Quantitation limit¶
The quantitation limit of an individual analytical procedure is the lowest amount of analyte in a sample which can be quantitatively determined with suitable precision and accuracy. The quantitation limit is a parameter of quantitative assays for low levels of compounds in sample matrices, and is used particularly for the determination of impurities and/or degradation products.
Linearity¶
The linearity of an analytical procedure is its ability (within a given range) to obtain test results which are directly proportional to the concentration (amount) of analyte in the sample.
Range¶
The range of an analytical procedure is the interval between the upper and lower concentration (amounts) of analyte in the sample (including these concentrations) for which it has been demonstrated that the analytical procedure has a suitable level of precision, accuracy and linearity.
Robustness¶
The robustness of an analytical procedure is a measure of its capacity to remain unaffected by small, but deliberate variations in method parameters and provides an indication of its reliability during normal usage.
