Régression¶

Corrélation¶

Lorsqu’on étudie des variables aléatoires, il peut être utile de vérifier leur indépendance ou bien la nature de leurs relations. L’analyse des relations entre variables est généralement réalisée à l’aide d’outils graphiques (nuages de points), combinés avec des indicateurs numériques (coefficients de corrélation).

Le plus connu des coefficients de corrélation est celui de Pearson. Il permet de quantifier l’intensité du lien entre les variables. Il est construit en faisant le rapport entre la covariance des variables X et Y et le produit des écart-types de X et Y. De cette manière on obtient des résultats compris entre -1 et 1.

\[r=\frac{\frac{1}{n}\sum_{i=1}^{n}\left((x_{i}-\overline{{x}})(y_{i}-\overline{{y}})\right)}{S_{x}\cdot S_{y}}\]

Un coefficient de corrélation proche de 1, met en évidence une corrélation positive forte : c’est à dire que les variables évoluent dans le même sens et qu’elles sont étroitement liées
Un coefficient de corrélation proche de -1, met en évidence une corrélation négative forte : c’est à dire que les variables évoluent dans le sens opposé et qu’elles sont étroitement liées
Un coefficient de corrélation proche de 0 montre que les variables ne sont pas corrélées linéairement. Ce n’est pas suffisant pour conclure à l’indépendance des variables.

Le coefficient de corrélation de Pearson étant très sensible à la présence de valeurs aberrantes, il est vivement conseillé de l’utiliser en complément d’un graphique, pour éviter les erreurs d’interprétation.

L’utilisation des coefficients de corrélation n’est pas spécifique aux variables continues, on peut aussi mesurer la corrélation de variables de rang. Le coefficient de Kendall par exemple, peut être utilisé pour quantifier les relations entre des rangs (ou classements) d’observations.

Lorsqu’on souhaite étudier la corrélation de plusieurs variables, on utlise généralement une matrice de nuages de points.

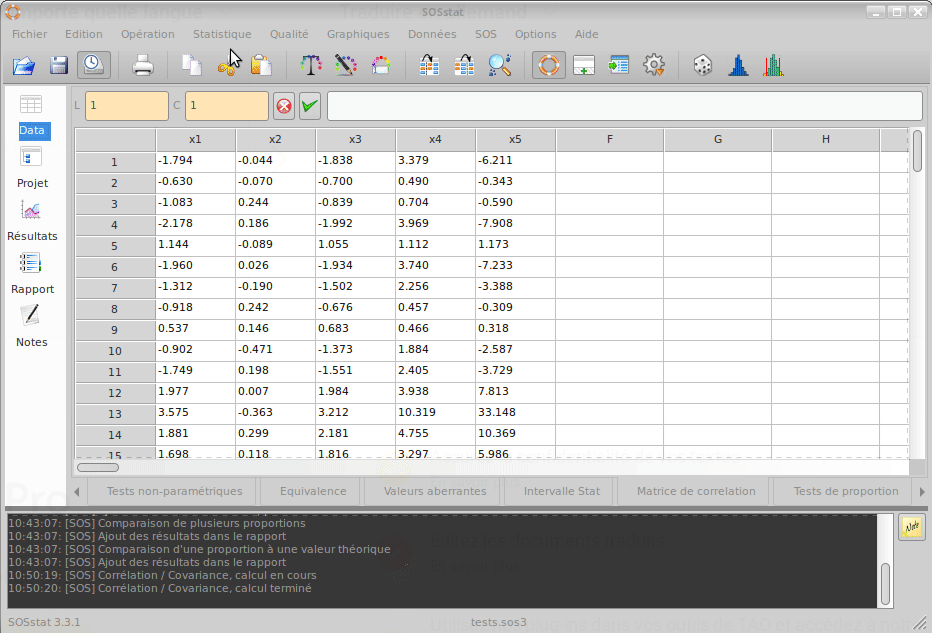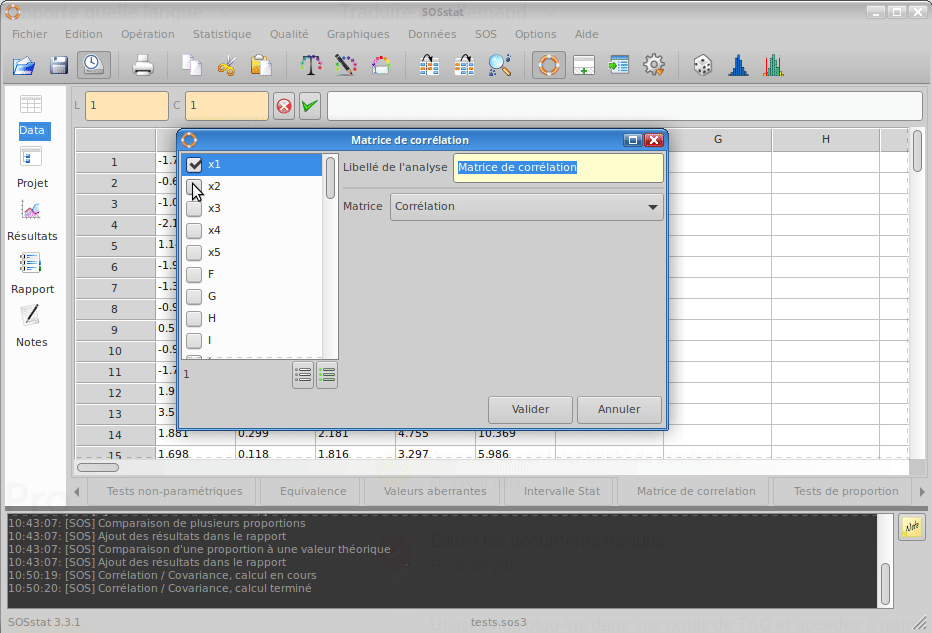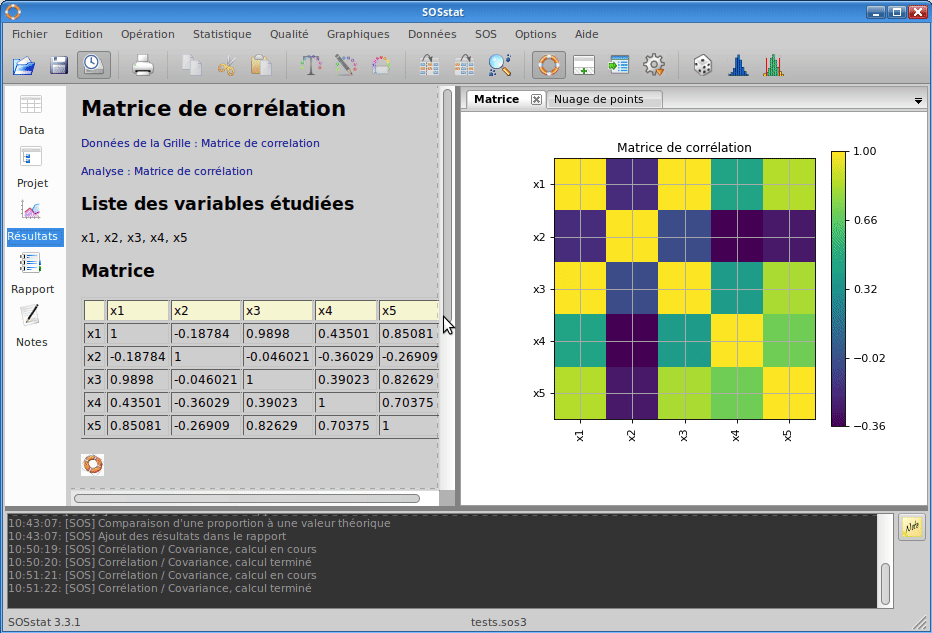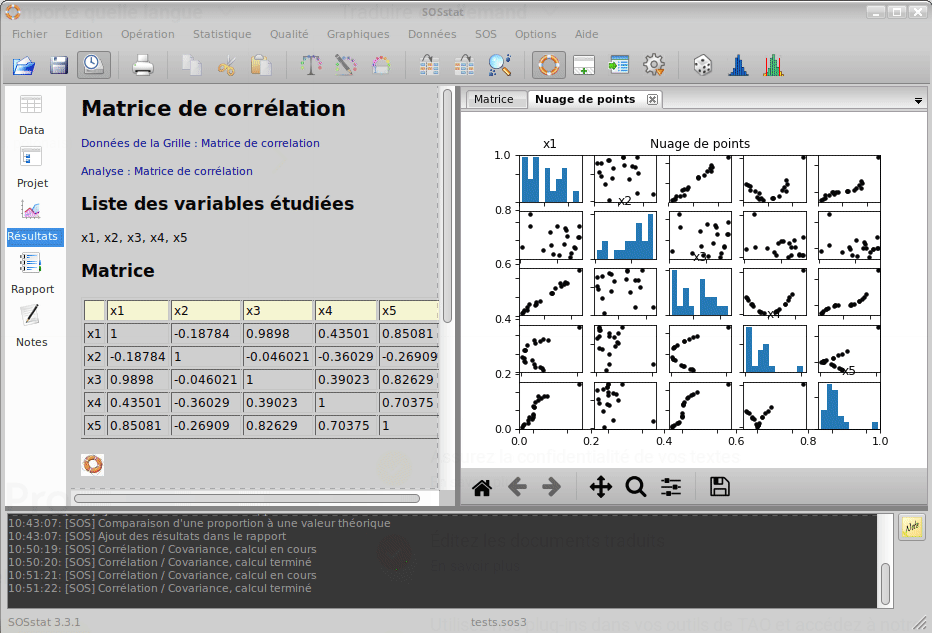
SOSstat permet d’analyser la corrélation de plusieurs variables. Les résultats de corrélation (ou de covariance) sont retournés dans une matrice, que l’on peut aussi visualiser sous forme d’une image avec une échelle de couleur correspondant au niveau de corrélation.

La régression simple¶

Après avoir démontré l’existence d’une corrélation entre deux variables aléatoires, on peut légitimement chercher à modéliser cette relation. La régression a pour objet de déterminer ce modèle. Même si les notions de corrélation et de régression sont souvent liées, il est bon de rappeler leurs différences.

La corrélation vise à quantifier l’intensité de la relation entre deux variables (leur degré de dépendance) afin de savoir si statistiquement ces valeurs évoluent dans le même sens ou en sens inverse. L’approche de la régression est un peu différente. A partir des couples de valeur (x,y), on cherche à construire un modèle tel que l’on puisse prévoir les valeurs de Y sachant les valeurs de X. On parle d’ailleurs de “variable explicative” pour X et de “variable expliquée” pour Y.

Estimation du modèle¶

Soient x et x deux variables aléatoires dépendantes. La prédiction de y notée \(\hat{y}\) est une fonction de la variable x : \(\hat{y}=f(x)\) . Pour pouvoir établir les coefficients du modèle, on utilise le critère d’optimisation des moindres carrés qui vise à minimiser l’erreur quadratique \((y-\hat{y})^{2}\) entre la valeur de y expérimentale et sa prédiction hat{y}.

Si on pose le modèle de prédiction linéaire sous la forme :

\[y=\alpha+\beta\cdot x\]

Alors l’application des moindres carrés permet d’établir (voir démonstration ci-dessous) les valeurs de \(\alpha\) et \(\beta\).

\[\beta=\frac{Cov(X,Y)}{Var(X)}=\rho\cdot\frac{\sigma_{Y}}{\sigma_{X}}\quad\alpha=E(Y)-\beta\cdot E(X)\]

Qualité du modèle¶

Une bonne application de la méthode des moindres carrés ne garantit malheureusement pas que le modèle soit de bonne qualité. En effet, la qualité des prédictions dépendra :

Du choix du modèle. On peut poser un modèle linéaire alors que la relation entre les variables n’est pas linéaire.
De l’intensité de la relation entre les deux variables. Si la dépendance de Y est faible vis-à-vis de X, alors il sera très difficile de prévoir les réalisations de Y sachant X.

Pour vérifier que le modèle a un caractère “explicatif” satisfaisant, on étudie la décomposition des variances. Dans la régression, on suppose que la variabilité totale constatée (SCT) est la somme de la variabilité expliquée par le modèle (SCM) et de la variabilité résiduelle (SCE), les écarts que le modèle ne peut prévoir. Cette relation s’exprime sous forme de somme d’écarts quadratiques.

\[SCT=SCE+SCM\]

où

SCT est la somme des carrés totale, c’est à dire la variabilité des mesures autour de la moyenne.
SCE est la somme des carrés des mesures autour des estimations, c’est à dire la variabilité résiduelle.
SCM est la somme des carrés des estimations autour de la moyenne, c’est à dire la variabilité expliquée par le modèle.

Cette décomposition des sources de variation permet d’établir le coefficient de détermination \(R^{2}\). Le coefficient de détermination représente le rapport entre la variabilité expliquée par le modèle et la variabilité totale :

\[R^{2}=\frac{\text{Variabilitée expliquée par la régression}}{\text{Variabilité totale}}\]

Comme on peut le voir dans l’animation ci-dessous, la mise en œuvre d’une régression simple est extrêmement facile dans SOSstat. Le graphique de régression peut afficher l’intervalle de confiance du modèle ainsi que l’intervalle de prédiction des observations. De plus, on procède à une analyse des résidus pour vérifier leur indépendance et leur normalité.

SOSstat fournit également des résultats numériques, avec notamment les coefficients du modèle (plusieurs modèles sont proposés) et le coefficient de détermination \((R^2)\). Un test de signification est appliqué sur le coefficient de corrélation des deux variables.

La régression multiple¶

Une extension naturelle de la régression simple, présentée précédemment, est la régression multiple ou multilinéaire qui permet d’identifier un modèle mettant en jeux plusieurs variables d’entrée.

Présentation du problème¶

Dans cette section, nous allons présenter le formalisme mathématique permettant de généraliser la méthode des moindres carrés à des systèmes comportant plusieurs variables. Les méthodes de calcul matriciel sont particulièrement appréciées pour résoudre des systèmes de n équations à n inconnues du fait de leur écriture synthétique et leur informatisation simple.

Lorsqu’on réalise une régression, notre objectif est d’identifier les paramètres d’un modèle mathématique. On peut considérer le cas d’un système comportant deux facteurs notés A et B que l’on souhaite représenter avec un modèle du premier ordre c’est à dire avec deux facteurs \(E_{A}\), \(E_{B}\) et une interaction \(I_{AB}\). Le modèle mathématique peut alors s’écrire :

\[Y=M+A\cdot E_{A}+B\cdot E_{B}+A\cdot B\cdot I_{AB}\]

Que l’on peut encore écrire d’une manière très générique :

\[Y=a_{0}+a_{1}\cdot x_{1}+a_{2}\cdot x_{2}+a_{12}\cdot x_{1}\cdot x_{2}\]

Ce modèle mathématique peut s’appliquer pour chaque combinaison des niveaux des facteurs (4 expériences si les deux facteurs ont chacun deux niveaux). Ainsi on peut exprimer les réponses en fonction de \(x_{1}\) et \(x_{2}\) qui prendront les valeurs -1 ou +1 (coordonnées centrées réduites) selon qu’ils sont au niveau mini ou maxi.

\[\begin{split}\begin{array}{c} y_{1}=a_{0}-a_{1}-a_{2}+a_{1}\cdot a_{2}\\ y_{2}=a_{0}+a_{1}-a_{2}-a_{1}\cdot a_{2}\\ y_{3}=a_{0}-a_{1}+a_{2}-a_{1}\cdot a_{2}\\ y_{4}=a_{0}+a_{1}+a_{2}+a_{1}\cdot a_{2} \end{array}\end{split}\]

Ce système de quatre équations peut être représenté sous forme matricielle en adoptant les notations suivantes:

Y est le vecteur des réponses du système

\[\begin{split}\mathbf{y}=\left[\begin{array}{c} y_{1}\\ y_{2}\\ y_{3}\\ y_{4} \end{array}\right]\end{split}\]

a est le vecteur des coefficients du modèle, c’est à dire les effets et interactions (qui sont organisés de manière bien précise).

\[\begin{split}\mathbf{a}=\left[\begin{array}{c} a_{0}\\ a_{1}\\ a_{2}\\ a_{12} \end{array}\right]\end{split}\]

X est la matrice d’expériences qui décrit la succession des expériences réalisées ou des observations des variables explicatives

\[\begin{split}\mathbf{X}=\left[\begin{array}{cccc} +1 & -1 & -1 & +1\\ +1 & +1 & -1 & -1\\ +1 & -1 & +1 & -1\\ +1 & +1 & +1 & +1 \end{array}\right]\end{split}\]

\[\mathbf{y=X\cdot a}\]

Dans cette représentation y et X sont connus et nous cherchons à identifier les coefficients de a.

Solution¶

Le modèle mathématique que nous avons cherché à identifier est purement théorique puisqu’il représente une relation déterministe entre la variable expliquée Y et les variables explicatives X. Pour prendre en compte les phénomènes aléatoires, on ajoute au modèle, un terme qui représente les résidus (Les résidus sont les écarts non pris en compte dans le modèle).

\[\mathbf{Y}=\mathbf{X}\cdot\mathbf{a}+\mathbf{e}\]

Pour résoudre ce système d’équation, on a recours à la technique de régression multiple ou multilinéaire. Cette dernière cherche une solution qui minimise la somme des carrés des écarts entre le modèle et les résultats expérimentaux (moindres carrés).

La solution d’un système linéaire avec le critère des moindres carrés est donnée par la relation:

\[\hat{\mathbf{a}}=(\mathbf{X}^{t}\mathbf{X})^{-1}\mathbf{X}^{t}\mathbf{y}\]

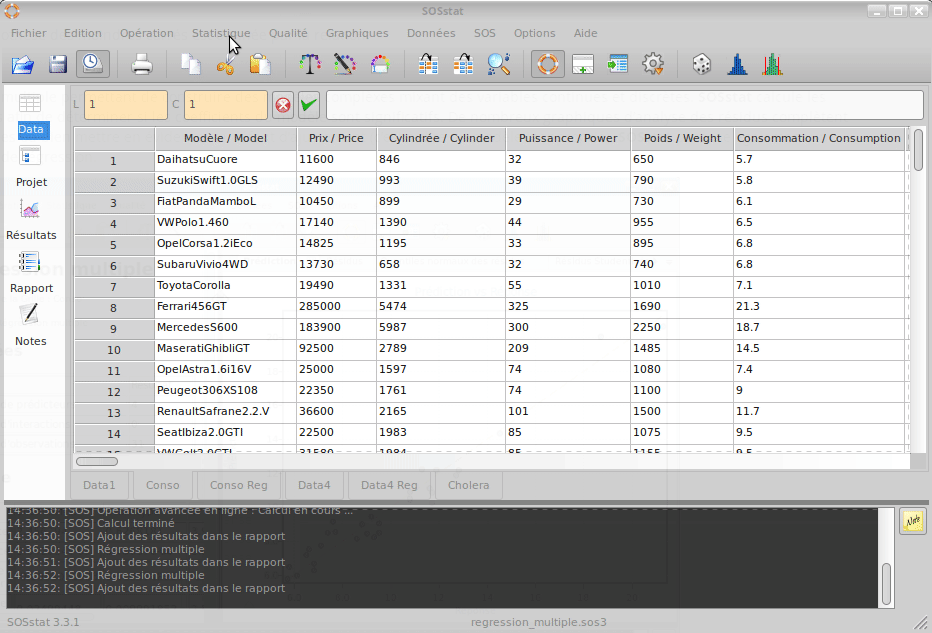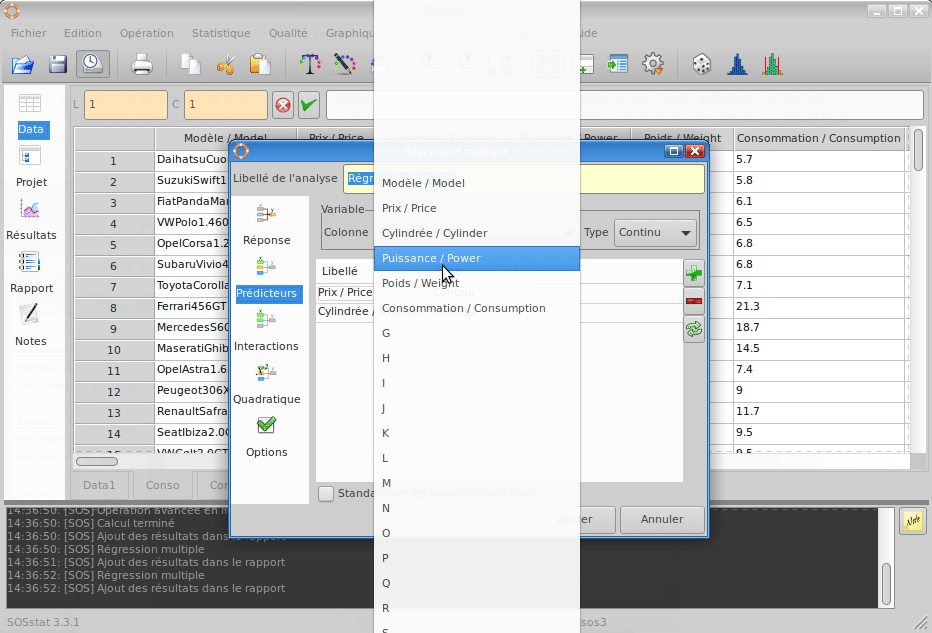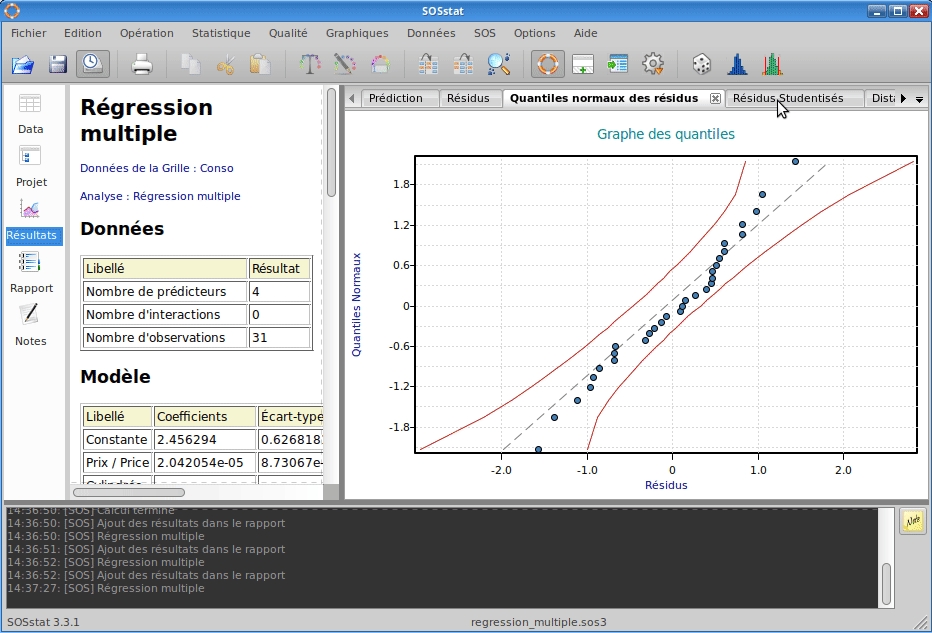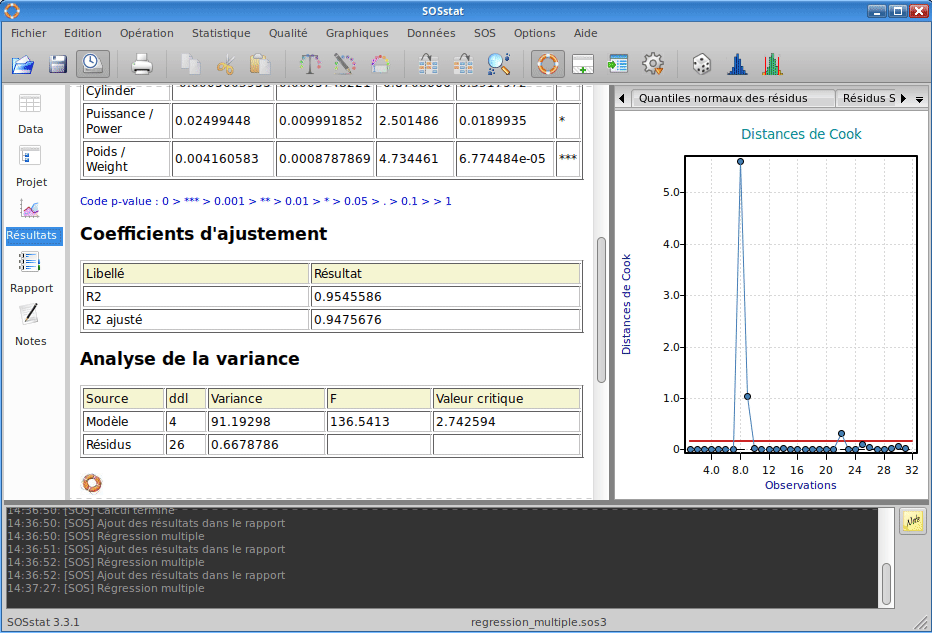
SOSstat propose un module de régression multiple permettant de construire des modèles complexes mixant des variables continues et discrètes. SOSstat calcule les coefficients du modèle et effectue des tests afin de déterminer si les coefficients du modèle sont significatifs. De nombreux graphiques d’analyse des résidus complètent les calculs afin d’identifier des valeurs isolées ou bien mettre en évidence un défaut d’ajustement (c’est à dire un modèle inapproprié).

SOSstat propose également un module de prédiction exploitant le modèle de régression. Ce dernier permet à l’utilisateur de trouver facilement la configuration des variables permettant de viser la réponse souhaitée.