- [FR]
- [EN]
- [DE]
- Site
- Page

Les plans d’expériences (en anglais, design of experiments ou DOE) se constituent d’une série d’expérimentations ou essais organisées, permettant d’acquérir de nouvelles connaissances en s’appuyant uniquement sur des résultats expérimentaux. Ainsi on modélise les relations entre les paramètres d’entrée (variables ou facteurs) du système étudié, et une (ou plusieurs) grandeur(s) de sortie, aussi appelée réponse. Le modèle mettant en œuvre une réponse \(y\) et des variables ou facteurs \(x_i\) peut se présenter sous une forme générique :
Les plans d’expériences sont utilisés dans de très nombreux domaines, ils peuvent par exemple :
SOSstat offre des fonctionnalités intuitives et simples pour la conception d’essais et l’analyse des résultats d’un plan d’expériences. Outre une bibliothèque complète de plans d’expériences classiques testés et éprouvés, SOSstat propose une fonction innovante de création de plans sur mesure qui permet d’adapter la conception des plans d’expériences aux contraintes expérimentales, tout en minimisant le nombre d’essais. Une fois les données collectées, SOSstat fournit une analyse simple et précise du modèle (avec de nombreux graphiques), les fonctions de prédiction, permettent ensuite de trouver les configurations qui répondent le mieux à notre problème.
Avant toute chose, il est important de noter, que la modélisation d’un système ne peut se faire en réalisant des essais sans stratégie préalable. En effet, l’organisation des essais a une influence déterminante sur la qualité du modèle, et donc des optimisations qui en découlent. Cette propriété n’étant pas intuitive, il est important de suivre la méthodologie des plans d’expériences pour garantir la qualité des résultats.
Voici quelques avantages de la méthodologie des plans d’expériences :
Au fil des années, les plans d’expériences se sont enrichis, de très nombreux outils pour répondre à une grande diversité de problématiques. Nous tenterons dans cette section, de faire un tour d’horizon des principales techniques expérimentales.

Différentes techniques de plans d’expériences disponibles dans SOSstat 3
Les plans Factoriels sont les plans les plus anciens. Ils permettent à la fois d’exploiter des variables continues ou catégorielles. Les modèles étudiés sont des modèles linéaires avec ou sans interaction. Les plans factoriels peuvent être utilisés dans deux situations :
Pour répondre à ces objectifs, on pourra exploiter plusieurs techniques :
Lorsque les variables d’entrée sont continues et que le modèle comporte un optimum local, il est préférable d’opter pour un modèle du second degré. C’est dans ce contexte que les plans de surface développent toute leur puissance. Ils permettent en effet d’optimiser un système en modélisant sa surface de réponse complexe. Les plans de surface les plus connus sont :
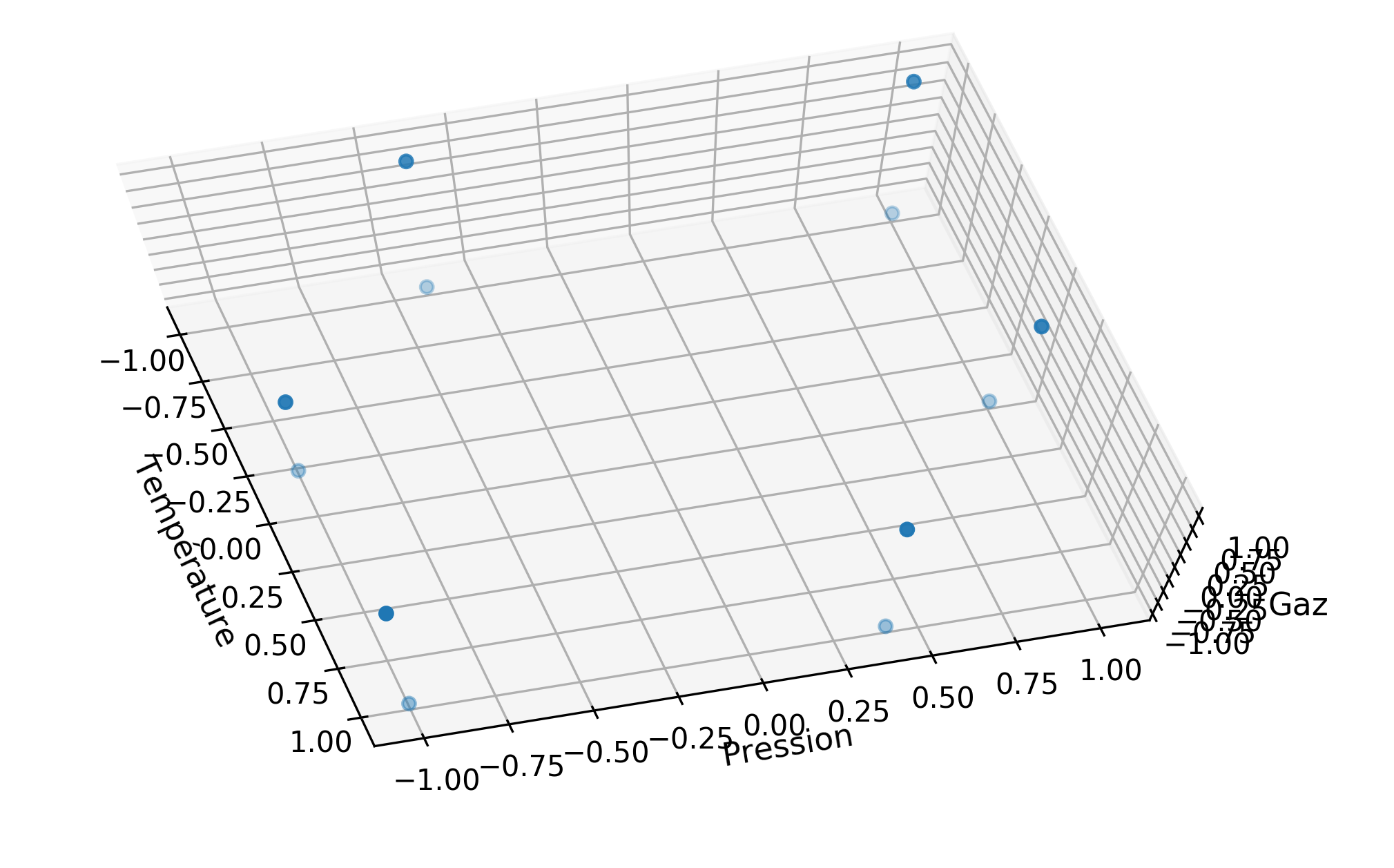
Répartition des essais dans un plan avec une contrainte sur la combinaison des facteurs température et pression.
Le cas des mélanges se rapproche de la problématique des plans de surface, dans la mesure où l’on est souvent dans un contexte d’optimisation d’un système non linéaire. La particularité des plans de mélange est de pouvoir prendre en compte les contraintes relationnelles entre les différents constituants du mélange. Ces techniques de plans d’expérience nécessitent d’être informatisées, car les matrices d’expériences ne sont pas orthogonales, de plus la définition des expériences nécessite d’établir au préalable le domaine d’expérimentation, qui dépend fortement des contraintes appliquées à chaque constituant (limitation du domaine expérimental).
La conception d’un plan d’expériences, commence toujours par un travail d’identification des facteurs supposés influents. Ensuite, l’expérimentateur détermine le nombre de niveaux pour chacun d’entre eux, ainsi que leurs modalités.
Lors de la conception d’un plan d’expériences, il est aussi important de déterminer les interactions à quantifier, mais dans le cas particulier des plans factoriels complets, cette étape n’est pas indispensable car toutes les interactions peuvent être quantifiées.
Dans l’exemple ci-dessous, on étudie 4 facteurs à deux niveaux sur un tour à commande numérique. Les 4 facteurs sont des paramètres de coupe, qui sont supposés avoir une influence sur la durée de vie de l’outil (réponse du système).
Les facteurs sont notés :
Le modèles implicite est donc (où M est la moyenne du modèle) :
Une fois le modèle défini (liste des facteurs avec leurs modalités et liste des interactions), SOSstat peut créer la matrice d’expériences. Dans cet exemple, il s’agit d’un plan factoriel complet. La matrice d’expériences affichée dans la grille, décrits l’enchaînement de combinaison des facteurs. Elle comporte les informations suivantes:
Le modèle se compose d’une constante, d’effets et d’interactions.
| Niv.1 | Niv.2 | |
|---|---|---|
| Vitesse avance | -2.075 | 2.075 |
| Profondeur | -3.425 | 3.425 |
| Vitesse de coupe | 6.2875 | -6.2875 |
| Debit | -0.1 | 0.1 |
On remarque que pour les facteurs à deux niveaux les effets sont opposés ( \(\sum \text{Effets}=0\) )..
Le tableau ci-dessous ne présente qu’une partie des interactions.
| Profondeur | Profondeur | Débit | ||||
|---|---|---|---|---|---|---|
| Niv1 | Niv2 | Niv1 | Niv2 | Niv1 | Niv2 | |
| Vitesse avance (Niv1) | 0.6 | -0.6 | 1.1125 | -1.1125 | 0.35 | -0.35 |
| Vitesse avance (Niv2) | -0.6 | 0.6 | -1.1125 | 1.1125 | -0.35 | 0.35 |
Pour les facteurs à deux niveaux, on observe une symétrie sur la valeur des interactions ( \(\sum \text{Interactions}=0\) ).
L’analyse de la variance est une étape importante de l’exploitation d’un plan d’expériences, car elle permet d’indentifier les termes significatifs du modèle. Seuls les paramètres ayant une p-Value inférieure à 5% sont gardés dans notre cas. (Cette analyse peut également se faire avec un tableau du test T).
| Source | ddl | S.Carrés | Variance | p-value | |
|---|---|---|---|---|---|
| Vitesse avance | 1 | 68.89 | 68.89 | 0.002232439 | * |
| Profondeur | 1 | 187.69 | 187.69 | 0.000219593 | *** |
| Vitesse de coupe | 1 | 632.523 | 632.523 | 1.14195e-05 | *** |
| Débit | 1 | 0.16 | 0.16 | 0.792806 | |
| Vitesse avance:Profondeur | 1 | 5.76 | 5.76 | 0.1573 | |
| Vitesse avance:Vitesse de coupe | 1 | 19.8025 | 19.8025 | 0.02738993 | * |
| Vitesse avance:Debit | 1 | 1.96 | 1.9 | 0.3766902 | |
| Profondeur:Vitesse de coupe | 1 | 40.3225 | 40.3225 | 0.007030376 | ** |
| Profondeur:Debit | 1 | 1.69 | 1.69 | 0.4091185 | |
| Vitesse de coupe:Debit | 1 | 6.5025 | 6.5025 | 0.1375826 | |
| Résidu | 5 | 10.42 | 2.084 | ||
Après exploitation de l’ANAVAR, le modèle qui initialement comportait 4 facteurs et 6 interactions, ne comporte plus que 3 facteurs et 2 interactions.; Ce modèle peut être utilisé directement pour optimiser le système (outil de prédiction de SOSstat)
Généralement les coefficients du modèle sont représentés graphiquement pour faciliter leur interprétation. Le graphe des effets représente l’évolution de la réponse moyenne en fonction des fluctuations individuelles de chaque facteur. Le graphe des interactions représente l’évolution des moyennes lorsque deux facteurs évoluent conjointement.
Sur le graphe des effets, on voit clairement l’influence prépondérante du facteur Vitesse de coupe.
Seul un graphe des interactions a été représenté. Il s’agit de l’interaction Profondeur:Vitesse de coupe (la plus significative). La présence de l’interaction se voit clairement, car les deux segments ne sont pas parallèles.
D’autre graphiques sont généralement proposés pour effectuer l’analyse des résidus
Il est assez courant qu’un plan d’expériences donne lieu à l’analyse de plusieurs réponses. Dans ce cas, nous avons à notre disposition autant de modèles que de réponses. Dans le cas de deux réponses, on a par exemple deux modèles \(y_1=f(x_1,x_2, ... , x_k)\) et \(y_2=f(x_1,x_2, ... , x_k)\) , qui mettent en jeu les mêmes facteurs. Comment optimiser ces deux réponses simultanément, sachant que les modèles sont différents, et que les objectifs pour \(y_1\) et \(y_2\) le sont certainement aussi ?
Pour réaliser un compromis raisonnable, nous allons décrire nos objectifs en utilisant des fonctions de désirabilité. Ces fonctions définissent l’atteinte de l’objectif par une valeur comprise entre 0 (non optimal) et 1 (optimal). Trois familles de fonctions sont utilisées, selon que l’on souhaite minimiser, maximiser une réponse ou bien viser une valeur particulière. Ces fonctions doivent être maximisées pour atteindre les objectifs. Pour cela, on fait la synthèse des objectifs assignés à chaque réponse, en construisant la fonction de désirabilité composite. En maximisant la fonction de désirabilité composite, on trouve le meilleur compromis.
Genichi Taguchi, ingénieur japonais, a développé la notion de robustesse en ingénierie dans les années 60. L’objectif est de pouvoir optimiser des systèmes, tout en s’assurant que leurs performances ne seront pas dégradées par des facteurs perturbateurs. Dans cette optique, Taguchi a alors l’idée de créer une variable de synthèse qui permet de rendre compte de l’atteinte des objectifs en termes de performance, et de robustesse vis-à-vis de facteurs perturbateurs. Cette variable est un ratio signal/bruit qui permet, selon les cas de maximiser ou minimiser une réponse, tout en minimisant la variance des réponses.
DUCLOS, E - Introduction aux plans d’expériences , LULU , 2019 , ISBN13 : 5800133354798
DROESBEKE Jean-Jacques , FINE Jeanne , SAPORTA Gilbert - Plans d’expériences, Applications à l’entreprise , Editions Technip , ISBN : 9782710807339
Goupy, J. - Introduction aux plans d’expériences , Dunod, 2017 , EAN13: 9782100778027
D.R. Cox, Nancy Reid - The Theory of the Design of Experiments , CRC Press, 6 juin 2000 - 336 pages
Douglas C. Montgomery - Design and Analysis of Experiments ,John Wiley & Sons, 2008 - 680 pages